Теорема о сумме углов треугольника

Эта теорема сформулирована и в учебнике Атанасяна Л.С. [3,с.66], и в учебнике Погорелова А.В. [14,с.54-55]. Доказательства этой теоремы в этих учебниках существенно не отличаются, а поэтому приведем ее доказательство, например, из учебника Погорелова А.В.

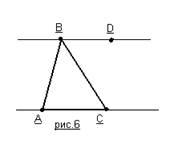
Теорема: Сумма углов треугольника равна 180°

Доказательство. Пусть АВС – данный треугольник. Проведем через вершину В прямую, параллельную прямой АС. Отметим на ней точку D так, чтобы точки А и D лежали по разные стороны от прямой ВС (рис.6).

Углы DВС и АСВ равны как внутренние накрест лежащие, образованные секущей ВС с параллельными прямыми АС и ВD. Поэтому сумма углов треугольника при вершинах В и С равна углу АВD. А сумма всех трех углов треугольника равна сумме углов АВD и ВАС. Так как эти углы внутренние односторонние для параллельных АС и ВD и секущей АВ, то их сумма равна 180°. Теорема доказана.

Идея этого доказательства состоит в проведение параллельной линии и обозначении равенства нужных углов. Реконструируем идею такого дополнительного построения, доказав эту теорему с использованием понятия о мысленном эксперименте. Доказательство теоремы с использованием мысленного эксперимента. Итак, предмет мысли нашего мысленного эксперимента – углы треугольника. Поместим его мысленно в такие условия, в которых его сущность может раскрыться с особой определенностью(1этап).

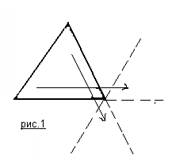
Такими условиями будут являться такое расположение углов треугольника, при котором все их три вершины будут совмещены в одной точке. Такое совмещение возможно, если допустить возможность «перемещения» углов, посредством движения сторон треугольника не меняя при этом угол наклона (рис.1). Такие перемещения по сути есть последующие мысленные трансформации (2 этап).

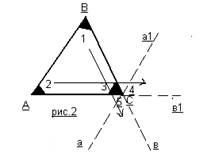
Производя обозначение углов и сторон треугольника (рис.2), углов получаемых при «перемещении», мы тем самым мысленно формируем ту среду, ту систему связей, в которую помещаем наш предмет мысли (3 этап).

Линия АВ «перемещаясь» по линии ВС и не меняя к ней угла наклона, переводит угол 1 в угол 5, а «перемещаясь» по линии АС, переводит угол 2 в угол 4. Поскольку при таком «перемещении» линия АВ не меняет угла наклона к линиям АС и ВС, то очевиден вывод: лучи а и а1 параллельны АВ и переходят друг в друга, а лучи в и в1 являются продолжением соответственно сторон ВС и АС. Так как угол 3 и угол между лучами в и в1 - вертикальные, то они равны. Сумма этих углов равна развернутому углу аа1 – а значит 180°.

Излагаемые доказательства, опирались на такие наглядно-чувственные идеализации: «сжатие», «растягивание», «скольжение», которые позволили особым образом трансформировать исходный геометрический объект и выделить его существенные характеристики, что характерно для мысленного эксперимента. При этом мысленный эксперимент выступает в роли определенного «креативного инструмента», способствующего появлению геометрического знания (например, о средней линии трапеции или об углах треугольника). Такие идеализации позволяют схватить в целом идею доказательства, идею проведения «дополнительного построения», что позволяет говорить о возможности более осознанного понимания школьниками процесса формально-дедуктивного доказательства геометрических теорем.

Мысленный эксперимент является одним из базовых методов получения и открытия геометрических теорем. Необходимо разработать методику передачи метода ученику. Остается открытым вопрос о приемлемом для «принятия» метода возрасте ученика, о «побочных эффектах» излагаемых таким образом доказательств.