Построение геометрического доказательства школьных теорем с использованием мысленного эксперимента

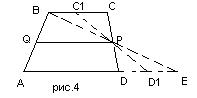
Производя обозначение вершин трапеции, треугольника, средней линии (рис.4), мы тем самым мысленно формируем ту среду, ту систему связей, в которую помещаем наш предмет мысли (3 этап).

Так как мы наложили условие сохранения прямизны, то, очевидно, что точки C и D боковой стороны CD, скользя по прямым AE и BC проходят одинаковые расстояния (длины). То есть CC1=DD1. Получается – происходит одинаковое растягивание отрезков CP и DP. Очевидно, что при таком скольжении их длины всегда равны (C1P = D1P и BP = EP). Значит отрезок QP – всегда средняя линия получаемого четырехугольника. Который, «при скольжении», стремится к совмещению двух своих вершин (точек С и В) и «превращению» в треугольник АВЕ.

QP – средняя линия треугольника АВЕ, а значит она параллельна стороне АЕ. Из этого вытекает параллельность сторонам AD и BC. Пройденные длины CB и DE – равны. Значит длина АЕ равна сумме длин AD и BC. Получается, что средняя линия QP трапеции ABCD параллельна основаниям BC и AD и равна их полусумме.