Построение геометрического доказательства школьных теорем с использованием мысленного эксперимента

Рассмотрим теорему о средней линии трапеции. Эта теорема по-разному представлена в школьных учебниках геометрии под авторством Погорелова А.В. и Атанасяна Л.С. В учебнике Атанасяна Л.С. [3,стр. 200 - 201] теорема доказывается через понятие вектора, а точнее через правило построения суммы нескольких векторов, называемое правилом многоугольника. Рассмотрим доказательством этой теоремы, приведенной в учебнике А.В. Погорелова [14, стр. 92], поскольку она доказывается с помощью дополнительного построения, и в этом смысле более «просто» и схоже с евклидовым. Приведем его дословно:

«Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Определение трапеции: трапеция - это четырехугольник, у которого только две противолежащие стороны параллельны.

Доказательство. Пусть ABCD – данная трапеция. Проведем через вершину В и середину Р боковой стороны CD прямую. Она пересекает прямую AD в некоторой точке Е.

Треугольники PBC и PED равны по второму признаку равенства треугольников. У них CP=DP по построению, углы при вершине Р равны как вертикальные, а углы РСВ и PDE равны как внутренние накрест лежащие при параллельных прямых ВС и АD и секущей СD.

Из равенства треугольников следует равенство сторон: РВ=РЕ, ВС=ЕD. Значит, средняя линия PQ трапеции является средней линией треугольника АВЕ. По свойству средней линии треугольника PQ || AE и отрезок PQ=1\2AE=1\2*(AD+BC). Теорема доказана».

Такое доказательство не позволяет «понять», откуда берется идея построения линии ВЕ. Тогда как именно в проведение этой линии и свернут акт мысленного эксперимента. Ведь после такого «дополнительного построения» остается лишь доказать равенство нужных треугольников. Наша задача состоит в «реконструкции» мысленного эксперимента как важного компонента доказательства.

Доказательство теоремы с использованием мысленного эксперимента.

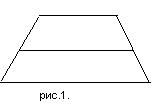
Итак, предмет мысли нашего мысленного эксперимента – отрезок, соединяющий середины боковых сторон трапеции с ее основаниями, т.е. средняя линия трапеции (рис.1.). Но мы не сможем что-либо узнать об этом отрезке, пока он находится в условиях трапеции. Мы должны поместить его мысленно в такие условия, в которых его сущность может раскрыться с особой определенностью (1этап).

Такими условиями является наделение одной из боковых сторон трапеции следующими идеальными свойствами:

- боковая сторона трапеции способна сжиматься и растягиваться, сохраняя при этом прямизну линии;

- точки боковой стороны, соприкасающиеся с основаниями, способны скользить по прямым линиям, содержащим основания трапеции. При этом точка, являющаяся серединой боковой стороны не должна менять своего расположения (т.е быть центром скольжения).

Такие сконструированные условия позволяют нам раскрыть сущность средней линии трапеции с особой определенностью (1 этап) – быть параллельной ее основаниям.

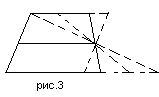
В самом деле: проводя последующие мысленные трансформации (2 этап) путем «вращения» идеализированной боковой стороны, мы будем получать различные варианты четырехугольника, с двумя параллельными сторонами, стремящегося в предельном случаи (совмещении двух вершин) к треугольнику (рис.3), где средняя линия трапеции сохраняет свойство быть средней линией получаемых фигур. Трансформация средней линии трапеции заключается в том, что она перестает быть средней линией трапеции, становясь средней линией другого геометрического объекта – треугольника.