Эксперимент

Отсюда получаем (1)

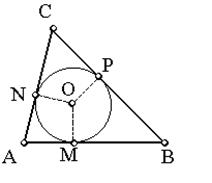
Построив отрезок х по этой формуле, проводим окружность (А, х), а затем две другие окружности (В, с – х) и (С, b – x).

Построение:

Строим отрезок по формуле

Строим окружность (А, х);

Строим окружность (В, с – х);

Строим окружность (С, b – х).

Доказательство: непосредственно следует из построения.

Исследование: Из формулы (1) находим:

(2)

Из этих формул всегда видно, что задача всегда разрешима, так как в треугольнике АВС c + b – a > 0, a + c – b > 0, a + b – c > 0 и отрезки x, y, z могут быть построены по формулам (2).

Формулы (2) дают единственные значения радиусов искомых окружностей, поэтому задача имеет единственное решение.

Домашнее задание: Построить отрезок, длина которого в выбранной системе измерения равна

Занятие 5

Тема: Метод параллельного переноса.

Цель: Выделить метод параллельного переноса.

Оборудование: Чертёжные инструменты.

План-конспект урока

Организационный момент.

Проверка домашнего задания.

Объяснение нового материала.

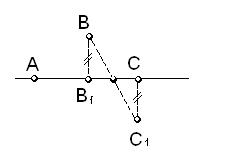
Преподаватель: Сущность метода параллельного переноса состоит в следующем: какую-либо часть искомой фигуры переносят или параллельно самой себе, или другим образом, но на такое расстояние, чтобы вновь полученная фигура могла быть построена или непосредственно, или легче, чем искомая фигура. Направление такого переноса зависит от условия задачи и должно быть выбрано так, чтобы во вновь полученную фигуру вошло, по возможности, большее количество данных. Давайте рассмотрим пример.

Задача 1

Постройте трапецию по заданным сторонам.

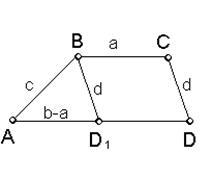
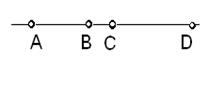
Анализ. Пусть трапеция АВСD построена, ВС= а, АD= b, AB= c, CD= d Выполним параллельный перенос, определяемый вектором СВ. Тогда сторона СD перейдёт в BD. Треугольник АВD можно построить по трём сторонам c, d, b-a (b>a).

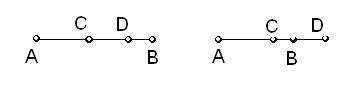
Затем продолжим отрезок АD на DD = a. Через точку В проведем прямую, параллельную АD и на ней отложим отрезок ВС= а. Соединим точки С и D. Полученная трапеция АВСD – искомая.

План построения очевиден.

Доказательство. В четырехугольнике АВСD BC параллельна AD, значит ABCD – трапеция в которой AB = c, AD =b, так как AD= b – a + a. BD= CD = d.

Исследование. Треугольник ABD можно построить по трём сторонам, если c – d < b – a < c + d. При этом условии однозначно выполнимы и все остальные шаги построения. Если неравенство c – d < b – a < c + d не выполняется, то задача при выбранных данных не имеет решения.

Задача 2

Построить параллелограмм по двум сторонам и углу между диагоналями.

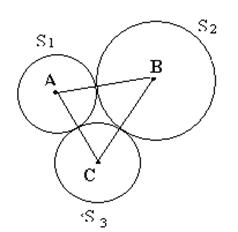
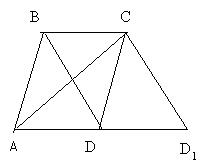
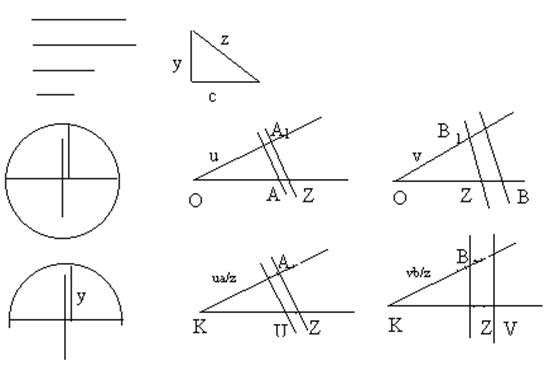
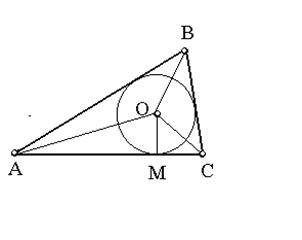
Анализ. Пусть ABCD – искомый параллелограмм и АВ = а, ВС = b, угол между диагоналями равен α. Если выполнить параллельный перенос на вектор ВС, то ТВС(D) = D1. Тогда AD1 = 2b, ÐACD1 = a, D – середина отрезка AD1 и DC = а. Значит, точка С принадлежит геометрическому месту точек из которых отрезок AD1 виден под углом a, и окружности S (D; a).

Построение.

AD1 = 2b;

F1 – геометрическое место точек из которых отрезок AD1 виден под углом a;

D – середина отрезка AD1;

S = S (D; a);

CÎF1Ç S (D; a);

B = TDA(C).

ABCD – искомый параллелограмм.

4. Домашнее задание: Постройте трапецию по основаниям и диагоналям.

Занятие 6

Тема: Метод подобия.

Цель: Выделить метод подобия.