Повышение уровня сформированности умений младших школьников решать задачи

Задание: Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.

Карточка №2. (для учащихся со средним уровнем обученности)

Задача: Оля собирала цветы: ромашки, васильки и колокольчики. Ромашек было , васильков было больше, чем ромашек, а колокольчиков – _, сколько ромашек и васильков вместе. Сколько всего?

Задание. Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.

Карточка №3. (для учащихся с высоким уровнем обученности)

Задача: Оля собирала цветы: ромашки, васильки и колокольчики. Ромашек было , васильков было , чем ромашек, а колокольчиков – _, сколько и вместе. Сколько _ ?

Задание. Дополни условие задачи так, чтобы ее решение задавалось выражением 10 + 10 × 4 + (10 + 10 × 4) и реши задачу.

Для проверки правильности выполнения задания целесообразно использовать интерактивную доску или мультимедийную презентацию.

Урок 68, задача №4 б.

Цель: повторить правило нахождения доли от числа, учить строить разнообразные вспомогательные модели к задаче.

Оборудование: учебник, мультимедийная аппаратура, слайды, карточки с выражениями.

Для украшения зала мальчики сделали 76 гирлянд из цветных фонариков. На украшение сцены пошло 16 гирлянд, третьей частью оставшихся гирлянд украсили стены, а остальными – вход в школу. Сколько гирлянд украшали вход в школу?

Дети сначала читают задачу, а затем отвечают на вопросы учителя:

¾ Какое изделие мальчики делали? (гирлянды)

¾ Сколько всего гирлянд они сделали? (76)

¾ Что украшали гирляндами дети? (сцену, стены и вход в школу)

¾ Сколько потребовалось гирлянд на сцену? (16)

¾ А на стены? (третья часть от оставшихся гирлянд)

¾ Что означает «третья часть числа»? (все оставшиеся гирлянды разделили на 3 равных части и взяли из них одну)

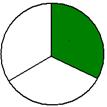
На доске вывешено несколько вспомогательных моделей задачи. Учитель говорит: «Найдите модель, подходящую к этой задаче» (см. рисунок №17). Учащиеся объясняют, почему нельзя выбрать модели №1 и №2, в качестве подходящей они выбирают модель №3.