Алгебраический метод

Сущность метода заключается в следующем. Решение задач на построение сводится к построению некоторого отрезка (или нескольких отрезков). Величину искомого отрезка выражают через величины известных отрезков с помощью формулы. Затем строят искомый отрезок по полученной формуле.

Пример 1. Провести окружность через две точки А и В так, чтобы длина касательной к ней, проведённой из точки С равнялась а.

Анализ. Пусть через точки А иВ проведена окружность так, что касательная к ней из точки С равняется а. Так как через три точки можно провести окружность, то проведём СВ и определим положение точки К. Полагаем СК = х и СВ = с; тогда по свойству касательной сх = а2.

Построение.

для построения х чертим полуокружность на ВС и дугу (С, а);

опустим LK ^ BC;

с× КС = а2; поэтому х = КС, и точка К будет искомая;

восстановив перпендикуляры из середин АВ и КВ до их пересечения найдём искомый центр О;

чертим окружность (О, ОА);

МС – искомая касательная.

Доказательство. МС2 = СВ×КС = 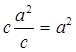и МС = а, как и требовалось.

Исследование. Выражение a £ с – условие существования решения нашей задачи, так как только при этом условии дуга (С, а) пересечёт окружность СLB.

Пример 2. Из вершин данного треугольника как из центров опишите три окружности, касающиеся попарно внешним образом.

Анализ. Пусть АВС – данный треугольник, а, b, c – его стороны, х, у, z – радиусы искомых окружностей. Тогда Поэтому откуда

Построение.

проводим окружность S1(A, x);

S2(B, c – x);

S3(C, b – x).

Доказательство. Найдём сумму радиусов окружностей S1 и S3:

= ВС.

Получили, что сумма радиусов равна расстоянию между их центрами, что и доказывает касание окружностей S2 и S3.

Исследование. Задача всегда однозначно разрешима, поскольку:

в треугольнике АВС сумма сторон , и поэтому отрезок х может быть построен;

, потому что (так как );

, так как .